StarWalker

Where my heart will take me

0%

Leetcode671-Second Minimum Node In a BinaryTree

Posted on Edited on In Views: Valine:
Solution Report of LeetCode Accepted

Description

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Example

Example 1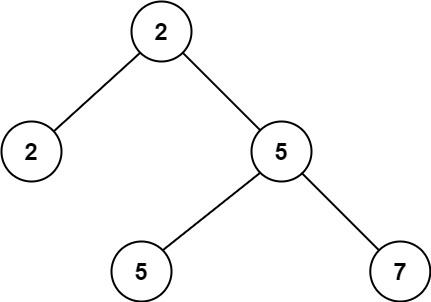

1
2
3
Input: root = [2,2,5,null,null,5,7]
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2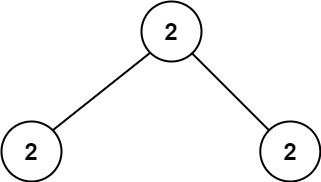

1
2
3
Input: root = [2,2,2]
Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

Constraints:

  • The number of nodes in the tree is in the range [1, 25].
  • 1 <= Node.val <= 231 - 1
  • root.val == min(root.left.val, root.right.val) for each internal node of the tree.

Solution

  • Time Complexity:
  • Space Complexity:

In this tree, the root should be the smallest node.

If the value of the children of the root node is not same, root val should be the smaller child value, but the larger one may not the second smallest one, cause the second smallest one may also in the subtree of the smaller value node.

Similar, if the two children value are the same, then calculate the second smallest value of each subtree, then compare them to find the smaller one as the second smallest value.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        if (root == null || root.left == null || root.right == null){
            return -1;
        }
        int left = root.left.val;
        int right = root.right.val;
        if (root.val ==  left){
            left = findSecondMinimumValue(root.left);
        }
        if (root.val == right){
            right = findSecondMinimumValue(root.right);
        }
        if (left == -1){
            return right;
        }
        if (right == -1){
            return left;
        }
        return Math.min(left, right);
    }
}