StarWalker

Where my heart will take me

0%

Leetcode351-Android Unlock Patterns

Posted on Edited on In Views: Valine:
Solution Report of LeetCode Acceptted

Description

Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an “unlock pattern” by connecting the dots in a specific sequence, forming a series of joined line segments where each segment’s endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

  • All the dots in the sequence are distinct.
  • If the line segment connecting two consecutive dots in the sequence passes through any other dot, the other dot must have previously appeared in the sequence. No jumps through non-selected dots are allowed.

Here are some example valid and invalid unlock patterns: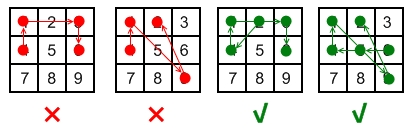

  • The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence.
  • The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
  • The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence.
  • The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

Example

Example 1:

1
2
Input: m = 1, n = 1
Output: 9

Example 2:
1
2
Input: m = 1, n = 2
Output: 65

Constraints:

1
1 <= m, n <= 9

Solution

  • Time Complexity:
  • Space Complexity: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {    
    public int numberOfPatterns(int m, int n) {
        // Skip array represents number to skip between two pairs
        int skip[][] = new int[10][10];
        skip[1][3] = skip[3][1] = 2;
        skip[1][7] = skip[7][1] = 4;
        skip[3][9] = skip[9][3] = 6;
        skip[7][9] = skip[9][7] = 8;
        skip[1][9] = skip[9][1] = skip[2][8] = skip[8][2] = skip[3][7] = skip[7][3] = skip[4][6] = skip[6][4] = 5;
        boolean vis[] = new boolean[10];
        int rst = 0;
        // DFS search each length from m to n
        for(int i = m; i <= n; ++i) {
            rst += DFS(vis, skip, 1, i - 1) * 4;    // 1, 3, 7, 9 are symmetric
            rst += DFS(vis, skip, 2, i - 1) * 4;    // 2, 4, 6, 8 are symmetric
            rst += DFS(vis, skip, 5, i - 1);        // 5
        }
        return rst;
    }
    
    // cur: the current position
    // remain: the steps remaining
    int DFS(boolean vis[], int[][] skip, int cur, int remain) {
        if(remain < 0) return 0;
        if(remain == 0) return 1;
        vis[cur] = true;
        int rst = 0;
        for(int i = 1; i <= 9; ++i) {
            // If vis[i] is not visited and (two numbers are adjacent or skip number is already visited)
            if(!vis[i] && (skip[cur][i] == 0 || (vis[skip[cur][i]]))) {
                rst += DFS(vis, skip, i, remain - 1);
            }
        }
        vis[cur] = false;
        return rst;
    }
}