
Description
We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You’re given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.
If you choose a job that ends at time X you will be able to start another job that starts at time X.
Example
Example 1: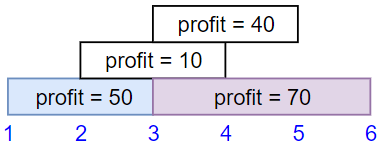
1
2
3
4Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2: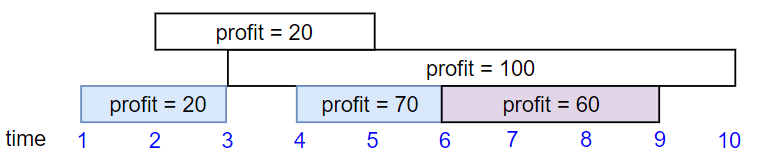
1
2
3
4Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Example 3:
1
2Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6
Constraints:
- 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
- 1 <= startTime[i] < endTime[i] <= 10^9
- 1 <= profit[i] <= 10^4
Solution
- Time Complexity: in total, sort , binary search
- Space Complexity:
Solution 1: DP + Binary Search
Sort the jobs by endTime.
dp[time] = profit means that within the first time duration,
we cam make at most profit money.
Intial dp[0] = 0, as we make profit = 0 at time = 0.
For each job = [s, e, p], where s,e,p are its start time, end time and profit,
Then the logic is similar to the knapsack problem.
If we don’t do this job, nothing will be changed.
If we do this job, binary search in the dp to find the largest profit we can make before start time s.
So we also know the maximum cuurent profit that we can make doing this job.
Compare with last element in the dp,
we make more money,
it worth doing this job,
then we add the pair of [e, cur] to the back of dp.
Otherwise, we’d like not to do this job.
1 | class Solution { |
Solution 2: DP + TreeMap
1 | public int jobScheduling(int[] startTime, int[] endTime, int[] profit) { |